Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

РОЗДІЛ 10. СТОХАСТИЧНЕ ПРОГРАМУВАННЯ

«Там на неведомых дорожках

Следы невиданных зверей…»

А. С. Пушкин

Повернувшись до наведеної в першому розділі класифікації задач математичного програмування, переконаємося, що в попередніх розділах досить детально були розглянуті основні види математичних моделей, які мають детермінований характер. Головною умовою побудови та використання детермінованих моделей є припущення про те, що всі початкові параметри задачі мають бути чітко визначеними. З погляду економіки така умова означає, що на етапі постановки задачі абсолютно точною є інформація стосовно всіх параметрів моделі. Однак загальновідомо, що економічні системи функціонують і розвиваються за умов невизначеності, тобто досить важко, а іноді і неможливо, мати точні значення деяких параметрів математичної моделі, особливо коли прогнозується розвиток процесів у майбутньому. Фактичні значення можуть суттєво відрізнятися від тих, які були взяті за основу при побудові математичних моделей та визначенні оптимальних планів, що породжує ризик прийнятих рішень. Невизначеність може бути різного ступеня залежно від того, яку інформацію ми маємо про досліджуваний процес чи явище. Якщо відомий розподіл відповідних параметрів, то для прийняття рішень використовують методи стохастичного програмування, суть яких полягає в тому, що відшукуючи оптимальне рішення , тобто значення керованих змінних, необхідно враховувати також вплив ряду випадкових чинників , керувати якими немає можливості. Наприклад, у разі планування діяльності сільськогосподарських підприємств є можливість точно передбачати площі посівів сільськогосподарських культур, рівні внесення добрив, поголів’я тварин (керовані змінні), але кінцевий результат діяльності у значній мірі залежить також від погодних умов, податкової та кредитної політики тощо (некеровані змінні).

Умовні екстремальні задачі, в яких параметри умов або складові розв’язку — випадкові величини, є предметом стохастичного програмування.

У стохастичному програмуванні частіше, ніж в інших розділах математичного програмування, значні труднощі виникають не лише за розроблення методів розв’язування задач, а також у разі їх постановки. Адже у постановці кожної задачі мають відображатися особливості прийняття рішень за умов невизначеності. Постановка задачі стохастичного програмування істотно залежить від її цільових засад та інформаційної структури.

10.1. Загальна математична постановка задачі стохастичного програмування

Типову задачу математичного програмування в детермінованій постановці формулюють так: визначити вектор 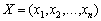, для компонент якого:

,

,

.

Якщо функції в даній задачі крім керованих параметрів Х залежать ще і від деяких випадкових величин , то маємо задачу стохастичного програмування:

,

,

, ,

де Ω — простір подій ω.

Залежно від можливості отримати та врахувати інформацію стосовно детермінованості (стохастичності) функцій , постановки задач стохастичного програмування можуть містити:

• стохастичні коефіцієнти цільової функції та детерміновані обмеження;
• детерміновані коефіцієнти цільової функції та стохастичні вільні члени і коефіцієнти системи обмежень;
• стохастичні коефіцієнти цільової функції, вільні члени і коефіцієнти системи обмежень.

Конкретні постановки задач стохастичного програмування мають свою специфіку. Передусім необхідно визначити:

• Детермінованим чи випадковим є вектор Х. Якщо вектор Х є детермінованим, то він не залежить від випадкових параметрів моделі. Якщо ж він випадковий, то тоді Х є функцією від ω — , тобто залежить від випадкових змінних.
• Як розуміти максимізацію (мінімізацію) цільової функції — як абсолютну (для всіх значень ) чи як максимізацію її математичного сподівання або деякої іншої ймовірнісної характеристики цієї функції (моди, медіани), або як мінімізацію середнього квадратичного відхилення? Наприклад, що краще мати: платню 500 ± 200 чи 450 ± 50? У першому разі платня може змінюватися в межах від 300 до 700 гривень, а у другому — лише від 400 до 500.
• Як виконуються обмеження: абсолютно для всіх чи в середньому, або з допустимими порушеннями, ймовірність яких мала?

При постановці задач стохастичного програмування необхідно виходити не лише з математичних міркувань, а й з економічного змісту та з врахуванням евристичних міркувань. Наприклад, детермінованість чи стохастичність вектора Х зумовлюється сутністю економічних, технологічних процесів тощо. Для сільськогосподарського підприємства, наприклад, вектор, що визначатиме площі посіву сільськогосподарських культур, обов’язково має бути детермінованим. Якщо ж шуканий вектор для того самого підприємства за тих самих умов визначатиме, приміром, обсяги кредитів, то його компоненти мають бути стохастичними величинами, бо достеменно невідомо, чи вони будуть отримані.

Методи розв’язування стохастичних задач поділяють на дві групи — прямі та непрямі.

Прямі методи використовують для розв’язування задач стохастичного програмування, коли існують способи побудови функцій і на базі інформації щодо параметра ω. Непрямими є методи зведення стохастичної задачі до задачі лінійного чи нелінійного програмування, тобто перехід до детермінованого аналога задачі стохастичного програмування.