Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

3.3. Основні теореми двоїстості та їх економічний зміст

Зв’язок між оптимальними розв’язками прямої та двоїстої задач встановлюють леми та теореми двоїстості. Розглянемо задачі (3.1)—(3.3) та (3.4)—(3.6) з економічною інтерпретацією, наведеною в § 3.1.

Лема 3.1 (основна нерівність теорії двоїстості). Якщо та — допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність

або . (3.7)

Доведення. Помножимо кожне рівняння системи (3.2) на відповідну змінну двоїстої задачі:

Маємо:

Підсумувавши праві і ліві частини нерівностей, отримаємо:

. (3.8)

Аналогічно перетворимо систему обмежень (3.5) двоїстої задачі:

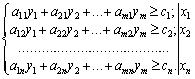
Підсумувавши після множення тут також ліві та праві частини, отримаємо нерівність:

(3.9)

Ліві частини нерівностей (3.8) та (3.9) збігаються, отже:

.

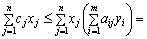
Нерівність (3.7) доведено.

Лема 3.2 (достатня умова оптимальності). Якщо та — допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність

(3.10)

то X*, Y* — оптимальні розв’язки відповідних задач.

Доведення. Нехай — допустимий план прямої задачі (3.1)—(3.3). Тоді на підставі нерівності (3.7) маємо: . За умовою задачі , отже

(3.11)

Оскільки за допущенням — довільний допустимий план прямої задачі, то нерівність (3.11) виконується для будь-якого з можливих розв’язків. Отже, маємо, що при цільова функція (3.1) набирає найбільшого значення, тобто є оптимальним розв’язком початкової задачі.

В аналогічний спосіб доводиться, що — оптимальний план двоїстої задачі.